The Fibonacci Sequence starts with the numbers 0 and 1, the sequence starts by adding 0+1 = 1, and then adding the last two numbers so that 1 + 1 = 2, 2+1 =3, 2+3=5. You end up with the sequence [0,1,1,2,3,5,8,13…]
https://en.wikipedia.org/wiki/Fibonacci_number
Option 1 – Iterative Solution
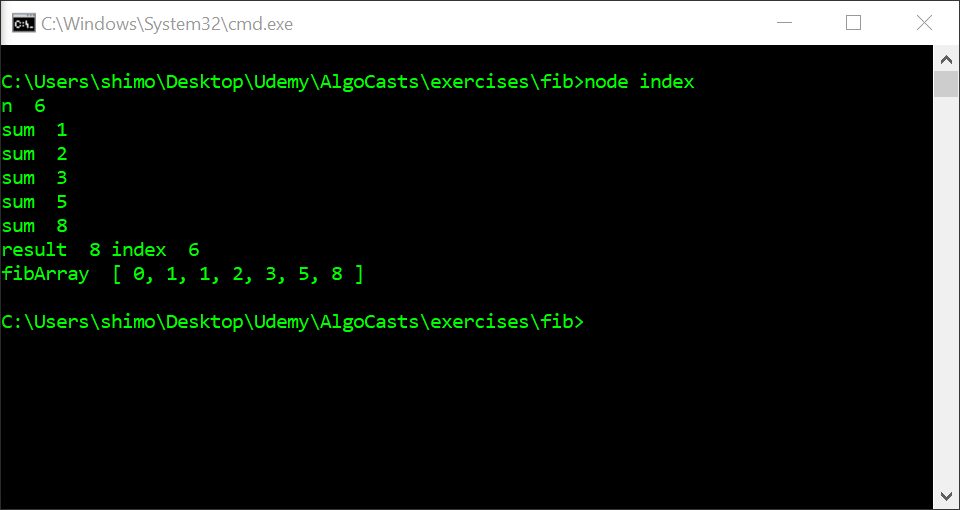
For my first attempt, I made an iterative solution using a for…loop. Since we have to start with 0 and 1, I created two variables – start and next – to store those, a sum variable to do the addition in, and an array (fibArray) to store the results. I then push start and next (0 and 1 into the array before I start the loop). Within the loop, I store start + next in sum (on the first loop 0+1 = 1) and I then push that into the array. Next, I set start = next and next = sum (on the first loop start = 1, and next = 2). After the loop is finished, I return the nth element of fibArray. In the example of n=6 that I did below, it will return 8 (fibArray = [0, 1, 1, 2, 3, 5, 8]).
I’m still going through the Stephen Grider course on Udemy. He just started covering runtime complexity, so I’ll add that here. For this solution, the runtime complexity = O(n) = linear.
// OPTION 1 - ITERATIVE SOLUTION
function fib(n) {
console.log('n ', n);
let start = 0;
let next = 1;
let sum=0;
const fibArray = [];
fibArray.push(start);
fibArray.push(next);
for (let i = 1; i<n; i++) {
sum = start + next
console.log('sum ', sum);
fibArray.push(sum);
start = next;
next = sum;
}
console.log('result ', fibArray[n], 'index ', n);
console.log('fibArray ', fibArray);
return(fibArray[n]);
}
fib(6);
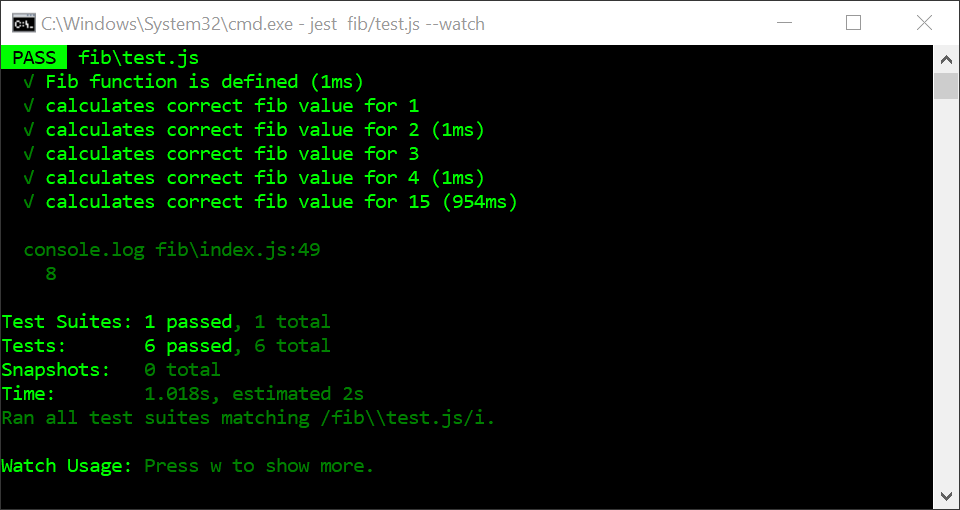
As you can see from the test results below, all the tests were finished in less than 1 millisecond (It doesn’t show a time for tests completed in less than a millisecond).

Option 2 – Recursive Solution
It’s hard to describe how recursion works. I found the CodeAcademy section on Javascript recursion useful as a review:
https://www.codecademy.com/en/courses/javascript-lesson-205/0/1
The course helps explain how the return values are stored in the stack every time the function is called. That is something I found confusing at first.
// OPTION 2 - RECURSIVE SOLUTION
function fib(n) {
if (n < 2) {
return n;
}
return fib(n - 1) + fib(n - 2);
}
const output = fib(6);
console.log(output); // output = 8
In the test results below, the recursive solution is much less efficient. For the iterative solution above, all tests including for, 15 finished in less than 1ms. Below the recursive test took 954 times longer — just shy of 1000ms / 1 second. The recursive solution has a run time complexity of exponential.
Option 3 – Recursive Solution Memoized
The solution above is not efficient because it calls the fib() function many times — multiple times for the same number. A solution to this is to create a memoize function to store the result of functions calls, and only make a new function call if the function hasn’t been previously called on that argument.
The new function memoize() calls our original fib() function — now renamed slowFib();
// OPTION 3 - RECURSIVE SOLUTION MEMOIZED
function memoize(func) {
const cache = {};
return function(...args) {
if (cache[args]) {
return cache[args];
}
const result = func.apply(this, args);
cache[args] = result;
return result;
};
}
function slowFib(n) {
if (n < 2) {
return n;
}
return fib(n - 1) + fib(n - 2);
}
const fib = memoize(slowFib);
All the tests now complete in 1ms or less, a great improvement on the recursive-only solution.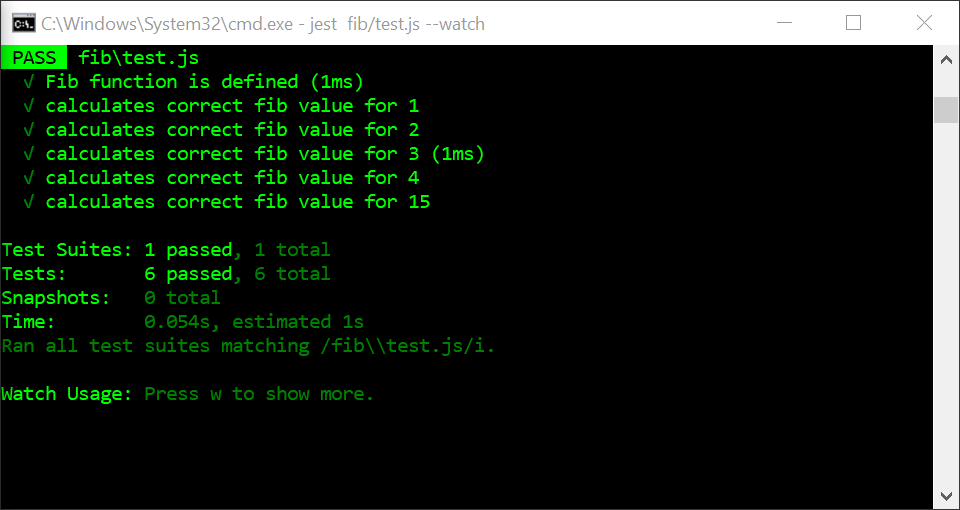
Solution 4 – Using While loop to Iterate to a Max number
The above solutions all take in “n” as the number of iterations in the sequence. Here in Solution 4, I have redone the problem using a while loop which takes in the max number I want to iterate to (instead of specifying the number of iterations).
// OPTION 4 - WHILE LOOP ITERATING TO MAX NUMBER
function fib(max) {
let start = 0;
let next = 1;
let sum=0;
const fibArray = [];
fibArray.push(start);
fibArray.push(next);
while (start + next <= max) {
sum = start + next
fibArray.push(sum);
start = next;
next = sum;
}
console.log('result ', fibArray[fibArray.length-1]);
console.log('fibArray ', fibArray);
return(fibArray[fibArray.length-1]);
}
const output = fib(100);
console.log(output);
When I run using max=100, it returns 89. The next number in the sequence is 144, which would be greater than our max of 100.